随着学习的深入，函数图像与性质在高三数学学习中占据了重要地位，函数图像是理解函数性质的重要工具，掌握函数图像与性质对于提高数学能力和解决实际问题具有重要意义，本文将深入探讨函数图像与性质的相关内容。

函数图像

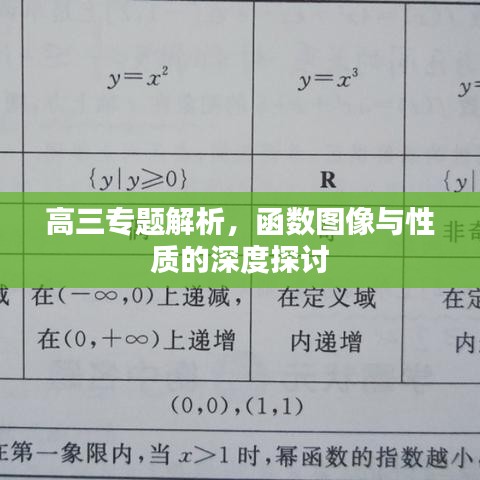
函数图像是函数值随自变量变化而变化的直观表现，常见的函数图像包括线性函数、二次函数、指数函数、对数函数等，这些函数图像具有不同的特征，如线性函数图像为直线，二次函数图像为抛物线等，掌握这些基本函数图像的特征，有助于快速识别复杂函数图像的基本类型。

函数性质

函数性质包括函数的定义域、值域、单调性、奇偶性、周期性等，这些性质对于理解函数图像具有重要意义，函数的定义域和值域决定了函数图像的范围，函数的单调性决定了函数图像的增减趋势，函数的奇偶性决定了函数图像关于原点或坐标轴的对称性，函数的周期性决定了函数图像的重复规律。

函数图像与性质的关系

函数图像与性质密切相关，通过观察函数图像，可以直观了解函数的性质；反之，通过了解函数的性质，可以预测和描绘函数图像，线性函数的斜率和截距决定了函数的增减趋势和图像与坐标轴的交点；二次函数的开口方向和顶点坐标决定了函数的最大值或最小值以及图像的对称轴。

专题学习建议

1、掌握基本函数图像与性质：了解各类基本函数的图像特征和性质，为复杂函数的学习打下基础。

2、联系实际：将函数图像与性质与实际生活问题相联系，提高解决实际问题的能力。

3、多练习：通过大量练习，加深对函数图像与性质的理解，提高解题技巧。

4、总结归纳：及时总结归纳学习过程中的经验和教训，形成自己的知识体系。

实例分析

以二次函数为例，二次函数的图像为抛物线，其开口方向、顶点坐标、对称轴等性质与函数的表达式密切相关，通过了解这些性质，可以预测二次函数的最大值或最小值，解决相关实际问题，在物理中的抛体运动，可以通过二次函数描述物体的运动轨迹，并预测物体的落点位置。

高三专题“函数图像与性质”是数学学习的重点内容之一，掌握函数图像与性质，对于提高数学能力和解决实际问题具有重要意义，在学习过程中，应注重掌握基本函数图像与性质，联系实际，多练习，及时总结归纳，形成自己的知识体系，希望通过本文的探讨，读者能对“函数图像与性质”有更深入的理解。