向量是数学中的一个重要概念，广泛应用于物理、工程、计算机科学等领域，向量的取值范围作为向量研究的一个重要专题，对于理解和掌握向量的性质和应用具有重要意义，本文将围绕“向量取值范围”这一主题展开讨论，探究向量的取值特点、影响因素以及确定向量取值范围的方法。

向量的基本概念

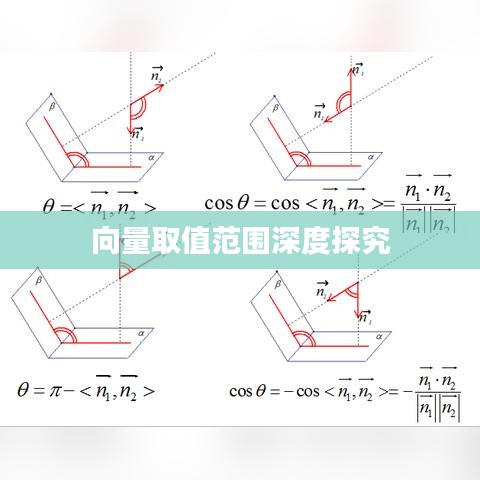
向量，又称为矢量，是一种具有大小和方向的量，在平面坐标系或空间坐标系中，向量可以用有向线段表示，向量的基本运算包括加法、数乘、点乘和叉乘等，向量的取值范围指的是向量在坐标系中可以取到的值的集合。

影响向量取值范围的因素

向量的取值范围受到多种因素的影响，主要包括以下几个方面：

1、向量的维度：二维向量和三维向量的取值范围不同，随着维度的增加，向量的取值范围也会扩大。

2、坐标系的类型：不同的坐标系（如笛卡尔坐标系、极坐标系等）会影响向量的表示和取值范围。

3、约束条件：实际问题中往往存在对向量取值的约束条件，如向量的模长、方向等。

确定向量取值范围的方法

确定向量取值范围的方法主要包括以下几种：

1、几何法：通过绘制向量的有向线段，观察其在坐标系中的位置，从而确定其取值范围。

2、代数法：通过解向量坐标的方程或不等式，确定向量的取值范围。

3、数值计算法：利用计算机进行数值计算，确定向量的可能取值。

向量取值范围的应用

向量取值范围的应用广泛，例如在物理中，可以用来描述物体的运动状态；在工程中，可以用来分析力、速度、加速度等；在计算机科学中，可以用来表示图像、声音等，掌握向量取值范围的相关知识，有助于解决实际问题。

案例分析

以二维平面中的向量为例，假设有一个向量A，其坐标范围为[-5,5]，即向量A的横坐标和纵坐标的取值范围均为[-5,5]，我们可以通过几何法绘制出向量A的有向线段，观察其在坐标系中的位置；也可以通过代数法解出向量A的坐标方程，确定其取值范围，在实际问题中，可以根据问题的约束条件，如物体的运动轨迹、力的方向等，确定向量的取值范围，从而进行分析和计算。

向量取值范围是向量研究的一个重要专题，对于理解和掌握向量的性质和应用具有重要意义，本文介绍了向量的基本概念、影响向量取值范围的因素、确定向量取值范围的方法以及向量取值范围的应用，通过案例分析，展示了如何在实际问题中应用向量取值范围的知识，希望本文能帮助读者更好地理解和掌握向量取值范围的相关知识。