等腰三角形是数学中一种重要的几何图形，具有独特的性质和应用价值，在日常生活和工业生产中，等腰三角形也展现出了广泛的应用场景，本文将围绕等腰三角形的定义、性质、判定方法以及实际应用等方面展开专题二的研究与探讨。

等腰三角形的定义和性质

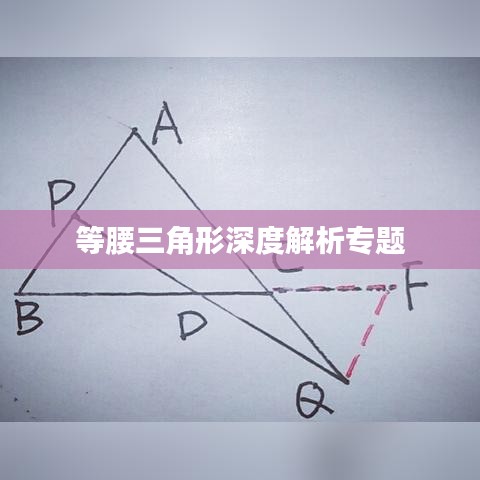
等腰三角形是两边长度相等的三角形，这两边被称为腰，而另一边则被称为底边，等腰三角形具有许多独特的性质，如两腰相等、两底角相等、三线合一等，这些性质为我们提供了判断一个三角形是否为等腰三角形的重要依据。

等腰三角形的判定方法

判定一个三角形是否为等腰三角形的方法有多种，其中常见的方法包括：两边相等判定法、两角相等判定法以及三线合一判定法等，在实际应用中，我们可以根据已知条件选择合适的判定方法来判断一个三角形是否为等腰三角形。

等腰三角形的应用

等腰三角形在实际生活中有着广泛的应用场景，在建筑设计中，利用等腰三角形的稳定性可以设计出稳固的屋顶结构；在机械工程中，等腰三角形的应用可以保证机械零件的精确度和稳定性；在几何学中，等腰三角形也是解决许多几何问题的重要工具。

专题二重点分析

在本专题中，我们将重点探讨等腰三角形的性质、判定方法以及应用，我们将深入研究等腰三角形的各种性质，如角平分线性质、垂直平分线性质等，我们将探讨多种判定方法的应用场景和适用范围，以便在实际问题中灵活选择，我们将结合实际应用案例，分析等腰三角形在实际生活和工作中的重要性。

实例解析

为了更好地理解等腰三角形的性质和应用，我们将通过实例进行解析，在建筑设计中，屋顶结构的稳定性问题可以通过运用等腰三角形的性质进行设计，在解决这类问题时，我们需要首先判断屋顶结构中的哪些部分可以构成等腰三角形，然后利用等腰三角形的稳定性原理进行设计，在机械工程中，等腰三角形的应用可以保证机械零件的精确度和稳定性，在齿轮设计中，通过合理设置齿轮的齿距和角度，可以形成等腰三角形，从而提高齿轮的承载能力和使用寿命。

研究展望

目前，关于等腰三角形的研究已经取得了许多成果，但在实际应用中仍有许多问题需要解决，我们可以进一步探讨等腰三角形在其他领域的应用，如计算机科学、物理学等，随着科技的发展，等腰三角形的相关算法和应用也将得到更多的关注和研究，在计算机图形学中，如何快速判断一个图形是否为等腰三角形，以及如何高效地进行等腰三角形的绘制等问题都值得深入研究。

本文围绕等腰三角形的定义、性质、判定方法以及实际应用等方面进行了专题二的研究与探讨，通过深入研究和分析，我们更好地理解了等腰三角形的相关知识和应用，我们将继续探索等腰三角形在其他领域的应用，为科技进步和社会发展做出贡献。